Ze zbioru wszystkich liczb naturalnych dwucyfrowych losujemy kolejno dwa razy po jednej liczbie bez zwracania. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że suma wylosowanych liczb będzie równa 30. Wynik zapisz w postaci ułamka zwykłego nieskracalnego.
Rozwiązanie:
Do obliczenia prawdopodobieństwa wykorzystujemy wzór z klasycznej definicji prawdopodobieństwa:$$P(A) = {{\left| A \right|} \over {\left| \Omega \right|}}$$Zbiór składa się z liczb naturalnych dwucyfrowych (jest ich 90 - od 10 do 99); losujemy 2 liczby bez zwracania, zatem:$$\left| \Omega \right| = 90 \cdot (90 - 1) = 90 \cdot 89 = 8010$$Suma wylosowanych liczb ma być równa 30, więc mogą to być tylko następujące pary:$$\left\{ {10,20} \right\},\left\{ {11,19} \right\},\left\{ {12,18} \right\},\left\{ {13,17} \right\},\left\{ {14,16} \right\},\left\{ {15,15} \right\},\left\{ {16,14} \right\},\left\{ {17,13} \right\},\left\{ {18,12} \right\},\left\{ {19,11} \right\}$$Jest ich 10, zatem:$$\eqalign{
& \left| A \right| = 10 \cr
& \cr
& P(A) = {{10} \over {8010}} = {1 \over {801}} \cr} $$
 Strona główna
Strona główna Arkusz
Arkusz

 $$\eqalign{
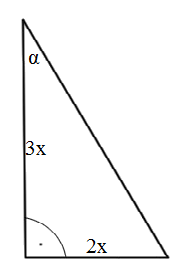
& {c^2} = {(3x)^2} + {(2x)^2} = 9{x^2} + 4{x^2} = 13{x^2} \cr
& c = \sqrt {13} x \cr
& \cr
& \sin \alpha = {{2x} \over {\sqrt {13} x}} = {{2\sqrt {13} } \over {13}} \cr} $$
$$\eqalign{
& {c^2} = {(3x)^2} + {(2x)^2} = 9{x^2} + 4{x^2} = 13{x^2} \cr
& c = \sqrt {13} x \cr
& \cr
& \sin \alpha = {{2x} \over {\sqrt {13} x}} = {{2\sqrt {13} } \over {13}} \cr} $$