Wskaż rysunek, na którym przedstawiono przedział, będący zbiorem wszystkich rozwiązań nierówności \( - 4 \le x - 1 \le 4\).
A.
B.
C.
D.
Rozwiązanie:
Odpowiedź C.
Nierówność \( - 4 \le x - 1 \le 4\) można zapisać za pomocą dwóch nierówności: $$ - 4 \le x - 1 \wedge x - 1 \le 4$$ Przekształcamy nierówności, aby po jednej stronie znajdował się \(x\) i otrzymujemy: $$x \ge - 3 \wedge x \le 5$$ Z tego wynika, iż zbiorem rozwiązań nierówności są liczby większe bądź równe -3 i mniejsze bądź równe 5, czyli wszystkie liczby leżące na osi między liczbami -3 a 5, łącznie z tymi liczbami.
 Strona główna
Strona główna Arkusz
Arkusz
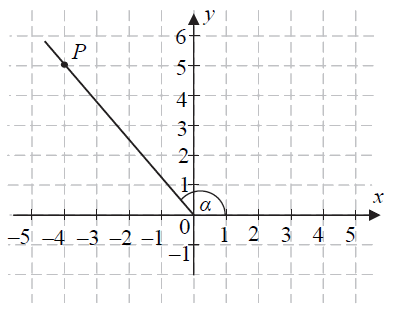 \(P=(-4,5)\)
\(P=(-4,5)\)