SYSTEMY ZAPISYWANIA LICZB

Co jest najmądrzejsze?
Liczba.
Co jest najpiękniejsze?
Harmonia.
Czym jest cały świat?
Liczbą i harmonią.
Pitagoras
Wprowadzenie

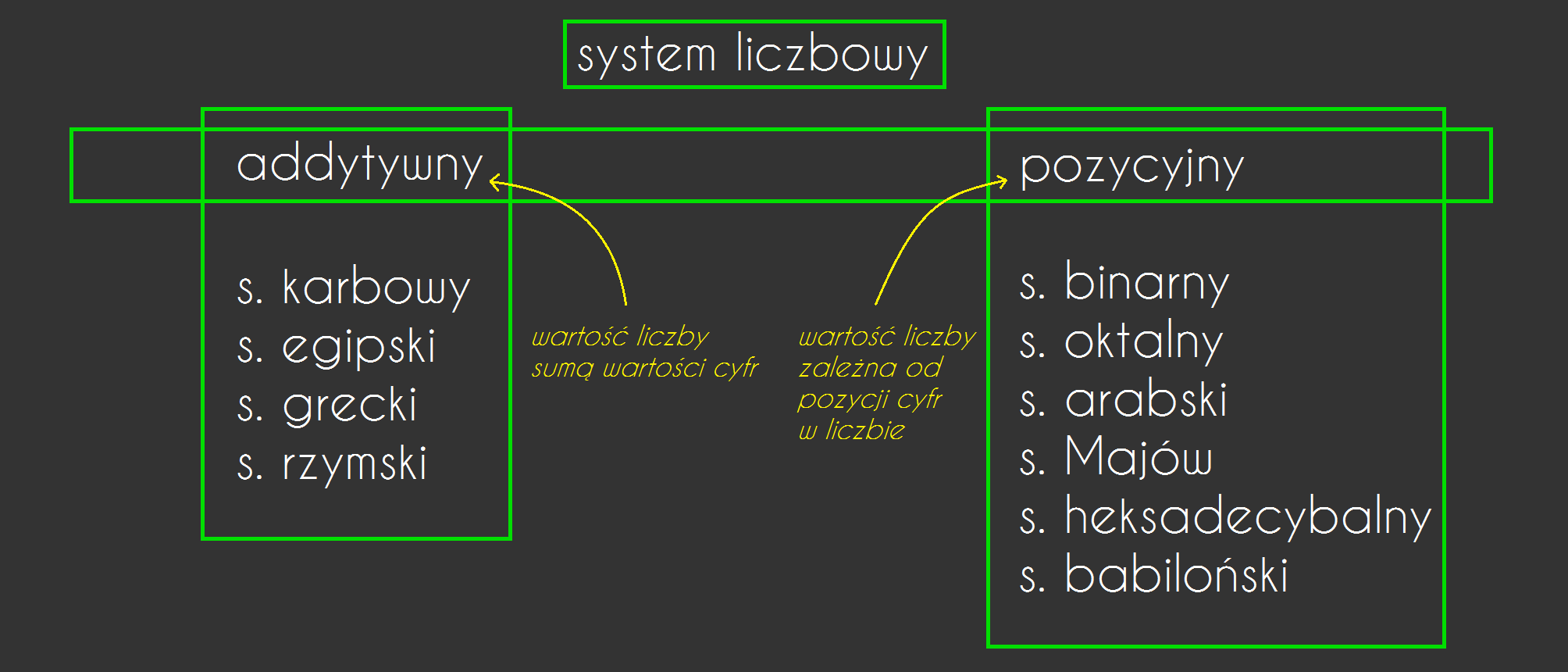
Systemem liczbowym nazywamy zbiór zasad, które określają sposób zapisu liczb, a także reguły działania na nich. Ważnym elementem każdego systemu są cyfry (skończony zbiór znaków). Systemy pozycyjne posiadają tzw. podstawę, która jest stałą cechą systemu.
Rodzaje systemów liczbowych
System karbowy
Pochodzi z ok 30 000 r. p.n.e. Polegał na żłobieniu nacięć na powierzchni kości. Ilość tych znaków, tzw. karbów, oznaczała liczbę.
|||| 4
|||||||||||| 12
|||||||||||||||||||||||||||||||| 32
W celu łatwiejszego odczytu większych liczb stosowano także inne oznaczenia, dla co piątej lub co dziesiątej kreski.
||||/||||/||||/||||/|||| 24
||||/||||X||||/||||X||||/||||X||||/||||X||||/||| 48
 Pobierz zadania
Pobierz zadania
System babiloński
Obecny już od XVIII w. p.n.e. stosowany po dzień dzisiejszy w mierzeniu jednostek czasu. Powstały w Babilonii, cyfry zapisywane za pomocą znaków pisma klinowego.
Liczby od 1 do 59 tworzono poprzez kombinacje cyfr wielokrotności 10 oraz cyfr 1-9:


= 19


= 37


= 52
Wartość liczb od 60 wzwyż to suma wartości poszczególnych znaków począwszy od prawej strony pomnożonych przez kolejne potęgi liczby 60 (60
0, 60
1, 60
2,...). Kwestię dot. braku znaku na liczbę 0 rozwiązywano pozostawiając puste pole w koniecznym miejscu.


= 69 = 1x60
1 + 9x60
0


= 186 = 3x60
1 + 6x60
0



= 3602 = 1x60
2 + 0x60
1 + 2x60
0
 Pobierz zadania
Pobierz zadania
System grecki
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| α' |
β' |
γ' |
δ' |
ε' |
ϝ' |
ζ' |
η' |
θ' |
| 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 |
| ι' |
κ' |
λ' |
μ' |
ν' |
ξ' |
ο' |
π' |
ϟ' |
| 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 |
| ρ' |
σ' |
τ' |
υ' |
φ' |
χ' |
ψ' |
ω' |
ϡ' |
Opraty na alfabecie greckim. Liczby zakończone specjalnym znakiem: ‘ tzw. kerają, w celu odróżnienia od zwykłych liter. Kolejne litery oznaczaly liczby od 1 do 10, wielokrotności 10 do 100 oraz wielokrotnosci 100 do 900. Ponieważ alfabet posiadał tylko 24 litery, konieczne było rozszerzonie alfabetu o 3 nowe znaki: ϝ (6), ϟ (90), ϡ (900).
ικε' = 100 + 20 + 5 = 125
υπγ' = 400 + 80 + 3 = 483
ωζ' = 800 + 7 = 807
Do zapisywania liczb o większej wartości stosowano: ͵ "lewą keraję", która stawiana przed znakiem zwiększała jego wartość 1000 razy.
͵βιε' = 2000 + 10 + 5 = 2015
͵σ͵μψθ' = 200 000 + 40 000 + 700 + 9 = 240 709
 Pobierz zadania
Pobierz zadania
System rzymski
System zapisu powszechny również w dzisiejszych czasach. Jednak oryginalna forma znaków miała inną postać.
System arabski
Podstawowy system liczbowy świata. Nazwywane systemem „arabskim”, gdyż to za pośrednictwem właśnie Arabów dotarł do Europy z Indii. Do zapisu stosowano cyfry od 0 do 9. Ich oryginalna forma była jednak odmienna:
Istatniały również inne warianty zapisu ze względu na etniczość indyjską.
System binarny
Powszechnie stosowany w informatyce i elektronice. Liczby tworzone za pomocą 2 cyfr: 0 i 1. Wartość w systemie dziesiętym jest sumą wartości kolejnych cyfr, począwszy od prawej strony pomnożonych przez kolejne potęgi liczby 2 (20, 21, 22, 23, ...).
10011 = 1x24 + 0x23 + 0x22 + 1x21 + 1x20 = 19
1011001 = 1x26 + 1x24 + 1x23 + 1x20 = 89
100001000011 = 1x211 + 1x26 + 1x21 + 1x20 = 2115
 Pobierz zadania
Pobierz zadania
System ósemkowy
Stosowany w informatyce z powodu łatwiejszego sposobu przeliczania niż system binarny. Do zapisu stosuje się 8 liczb: od 0 do 7. Wartość w systemie dziesiętym jest sumą wartości kolejnych cyfr, począwszy od prawej strony pomnożonych przez kolejne potęgi liczby 8 (80, 81, 82, 83, ...).
27 = 2x81 + 7x80 = 16 + 7 = 23
165 = 1x82 + 6x81 + 5x80 = 64 + 48 + 5 = 117
2371 = 2x83 + 3x82 + 7x81 + 1x80 = 1273
 Pobierz zadania
Pobierz zadania
System heksadecybalny
Ma zastosowanie w programowaniu. Do zapisu liczb stosuje sie 10 cyfr: od 0 do 9 oraz 6 znaków (liter z łacińskiego alfabetu): A, B, C, D, E, F, które odpowiadają kolejno liczbom: od 10 do 15. Wartość w systemie dziesiętym jest sumą wartości kolejnych znaków, począwszy od prawej strony pomnożonych przez kolejne potęgi liczby 16 (160, 161, 162, 163, ...).
B5 = 11x161 + 5x160 = 176 + 80 = 256
3FA = 3x162 + 15x161 + 10x160 = 768 + 240 + 10 = 1018
1C29 = 1x163 + 12x162 + 2x161 + 9x160 = 4649
 Pobierz zadania
Pobierz zadania
System Fibonacciego
Ciąg Fibonacciego
Słynny ciąg składa się z liczb naturalnych, począwszy od 0 i 1, po czym każda kolejna liczba ciągu jest sumą wartości dwóch poprzednich liczb.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, ...
Może być określony w następujący sposób:
Fn = 0 ⇔ n = 0
Fn = 1 ⇔ n = 1
Fn = Fn-1 + Fn-2 ⇔ n ≥ 2
Spirala Fibonacciego
 Charakterystycznym elementem to własność polegająca na tym, że liczby Fibonacciego są długościami boków ciągu kwadratów dorysowywanych do siebie, które mogą być do siebie dokładane w nieskończoność.
Charakterystycznym elementem to własność polegająca na tym, że liczby Fibonacciego są długościami boków ciągu kwadratów dorysowywanych do siebie, które mogą być do siebie dokładane w nieskończoność.
 W wyniku rysowania łuków łączących kolejne przeciwległe wierzchołki kwadratów otrzymujemy spiralę Fibonacciego. W tym wypadku liczby Fibonacciego tworzą kolejne promienie ćwiartek okręgów.
W wyniku rysowania łuków łączących kolejne przeciwległe wierzchołki kwadratów otrzymujemy spiralę Fibonacciego. W tym wypadku liczby Fibonacciego tworzą kolejne promienie ćwiartek okręgów.
System Fibonacciego
Jest odmianą systemu binarnego - wartośći pozycji są kolejnymi liczbami Fibonacciego, wyłączając początkowe 0 i 1 (czyli: 1, 2, 3, 5, 8, 13, 21, itd.).
101 = 1x3 + 0x2 + 1x1 = 3+1 = 4
100101 = 1x13 + 1x3 + 1x1 = 13+3+1 = 17
101000101 = 1x55 + 1x21 + 1x3 + 1x1 = 55+21+3+1 = 80
Ponieważ w takim zapisie istnieje możliwość zakodowania liczby na dwa sposoby (np. 100 = 3 oraz 11 = 3), dwie kolejne cyfry liczby nie mogą być 1.
Źródła:
grafika przetworzona z portalu www.freeimages.com :
http://www.freeimages.com/photo/digital-dreams-1155914
http://www.freeimages.com/photo/clock-1-1422903
tekst opracowany na podstawie m.in.:
Georges Ifrah, „The Universal History of Numbers: From Prehistory to the Invention of the Computer”, Wiley, 2000 r.
Edward Jerzy Pokorny, „Narodziny liczby”, Iskry, 1957 r.
a także serwisów internetowych:
http://www.math.edu.pl/systemy-liczbowe
http://www.programuj.com/artykuly/rozne/sysliczb.php
http://eduinf.waw.pl/inf/alg/001_search/0025.php
© 2015 Michał Kierat




 Pobierz zadania
Pobierz zadania















































 Charakterystycznym elementem to własność polegająca na tym, że liczby Fibonacciego są długościami boków ciągu kwadratów dorysowywanych do siebie, które mogą być do siebie dokładane w nieskończoność.
Charakterystycznym elementem to własność polegająca na tym, że liczby Fibonacciego są długościami boków ciągu kwadratów dorysowywanych do siebie, które mogą być do siebie dokładane w nieskończoność. W wyniku rysowania łuków łączących kolejne przeciwległe wierzchołki kwadratów otrzymujemy spiralę Fibonacciego. W tym wypadku liczby Fibonacciego tworzą kolejne promienie ćwiartek okręgów.
W wyniku rysowania łuków łączących kolejne przeciwległe wierzchołki kwadratów otrzymujemy spiralę Fibonacciego. W tym wypadku liczby Fibonacciego tworzą kolejne promienie ćwiartek okręgów.